مقدمه‌ای بر DHT و الگوریتم Kademlia

یکی از مسائل مهم در علوم کامپیوتر ذخیره و بازیابی اطلاعات است. روش‌های مختلفی برای ذخیره اطلاعات در سیستم‌های کامپیوتری وجود دارد. ساده‌ترین این روش‌ها ذخیره‌سازی خطی داده در خانه‌های حافظه مثل یک آرایه ساده است. اگر داده‌ها تعداد کمی داشته باشند این روش روش قابل قبولی به نظر میرسد اما اگر قصد ذخیره تعداد زیادی داده داشته باشیم مشکلات ذخیره‌سازی خطی خودشون رو نشون میدن. مثلا پیدا کردن یک داده در آرایه بزرگ بدون پایبندی به قاعده خاصی در زمان ذخیره سازی از مرتبه ‍$O(n)$ است.

Hash Table یکی از روش‌های ذخیره اطلاعات با تعداد زیاد با امکان بازیابی سریع است. روش عملکرد یک Hash Table خیلی ساده است. داده‌ها بر اساس یک کلید و با نظمی مشخص در آرایه ذخیره می‌شوند تا هنگام بازیابی نیاز به جستجوی همه آرایه نباشد و بتوان خیلی سریع سراغ نزدیک‌ترین مکان ممکن به داده مورد نظر رسید.

اما اگر همزمان با حجم زیادی داده هم سر و کار داشته باشیم یا ذاتا داده‌ها در یک سیستم کامپیوتری نباشند و در سطح یک شبکه کامپیوتری پخش شده باشند کار دشوارتر هم می‌شود. راه حلی که اینجا خیلی خوب مشکل را حل میکند DHT است. در DHT ها یک قاعده ریاضی برای ذخیره و جستجوی محتوا در شبکه اجرا می‌شود و همه در آن مشارکت میکنند در نتیجه نیازی نیست همه، کل لیست محتوا و آدرس آنها را نگهداری کنند و در نتیجه همه چیز خیلی سریع‌تر و راحتتر میشود.

Hash Table

ایده اصلی Hash Table خیلی ساده است. برای هر دیتا یک شناسه یا کلید تعریف میکنیم (مثلا خود دیتا میتونه کلید باشه یا حتی بهش اسم بدیم) و شناسه رو به روشی به یک عدد تبدیل کنیم و دیتا رو توی مکانی که اون عدد نشون میده ذخیره کنیم. اینطوری برای پیدا کردن دیتا میتونیم از روی شناسه جاش رو حساب کنیم و مستقیم بریم سراغش و دیگه نیازی به جستجو نیست. یک روش خیلی ساده برای ساخت عدد اینه که اسم کلید رو به کاراکتر هاش بشکنیم و کد اسکی کاراکترها رو جمع بزنیم و برای اینکه از لیست بیرون نزنه باقیمانده‌اش به سایز لیست رو حساب کنیم. مثلا اگر یک آرایه 100 تایی داشته باشیم و بخواهیم مقدار test رو توش ذخیره کنیم: \[ t,e,s,t \longrightarrow 116,101,115,116 \] \[ 116+101+115+116 = 448 \] \[ 448 \mod 100 = 48 \]

پس test در خونه 48 آرایه 100 تایی ذخیره میشه. طبیعتا به راحتی ممکنه برای دو مقدار هش مشابهی به دست آید. به این اتفاق collision گفته میشود و یک الگوریتم خوب هش باید تا حد ممکن از ایجاد کالیژن اجتناب کند. در صورت ایجاد کالیژن الگوریتم باید به نحوی ذخیره مقادیری که هش مشابه دارند را مدیریت کند. مثلا اگر یک خانه خالی بعد از آدرس را به عنوان جانشین انتخاب کنید (به این روش Open Addressing گفته میشود) احتمال تجمع مقادیر کنار هم وجود دارد (به آن clustering گفته می‌شود) و نتیجه آن استفاده غیر بهینه از فضا خواهد بود. همینطور میتوان همه مقادیر با هش مشابه در یک خانه (مثلا توسط LinkedList ها) ذخیره کرد (به آنهم Chaining گفته میشود). طبیعتا فضای محل ذخیره‌سازی باید آنقدر بزرگ باشد تا چنین مشکلاتی به حداقل برسد و همینطور یک الگوریتم خوب باید بتواند مقادیر را تا حد ممکن به صورت همگن و یکنواخت در فضای هش پخش کند.

DHT (Distributed Hash Table)

بیایید فرض کنیم یک سری دوست میخواهند کلکسیون فیلم‌هاشون رو با همدیگر توی شبکه به اشتراک بگذارند. اونا میتونن یک لیست از IP و فیلم ‌های همدیگه داشته باشند و هر زمان فیلمی رو خواستن به کامپیوتری که اونو داره وصل بشن و فیلم رو کپی کنن. مشکل وقتی پیش میاد که هر کس بخواد فیلم جدیدی اضافه کند یا فیلم قدیمی را پاک کند یا آدرس کامپیوترش عوض شود. اینجا باید به بقیه اطلاع دهد. شاید یک راه ساده این باشد که یک پیام به همه ارسال کند و تغییرات را گزارش کند، اما این روش فقط وقتی تعداد تغییرات و اعضای شبکه کم باشد امکان پذیر است. اگر تعداد تغییرات خیلی زیاد باشد کل شبکه همیشه با پیام‌های تغییر اشغال میشود. همینطور اگر تعداد افراد و فیلم‌ها زیاد شود حجم خود لیست زیاد شده و در نتیجه جستجو در آن بسیار زمان‌بر خواهد شد و حتی اگر بخواهیم کل اینترنت را به این شیوه به همدیگر متصل کنیم اساسا هر کامپیوتر نمیتونه لیستی به این بزرگی را ذخیره کنه.

راه حلی که در سالهای بعد از 2001 برای حل این مشکلات مکانیابی ارائه شد به نام DHT شناخته می‌شود، در واقع DHT همان ذخیره ساختارمند از طریق ایده اصلی HashTable به صورت توزیع شده است. تعداد زیادی الگوریتم DHT وجود دارد که معروفترین آنها CAN، Chrod، Pastry، Tapestry و Kademlia هستند.

در مجموعه الگوریتم‌های توزیع شده مسیر یابی و ذخیره مشارکتی محتوا به دو دسته ساختارمند و بدون‌ساختار تقسیم می‌شوند و تفاوت اصلی آنها در وجود یک قاعده ریاضی برای آدرس‌دهی به کامپیوترها و محتواها است. DHT ها از دسته الگوریتم‌های ساختارمند بحساب می‌آیند و اساس کار آنها بر این اساس استوار است که تمام آدرس‌ها در یک جا نگهداری نشود و کاربران با کمک همدیگه آدرس‌ها را نگهداری و بازیابی کنند. بهترین الگوریتم‌های DHT میتوانند در عمل مرتبه زمانی لگاریتمی در عمل جستجو، مسیریابی و ذخیره سازی را ارائه کنند.

Kademlia

در بین الگوریتم‌های DHT الگوریتم Kademlia یکی از بهترین الگوریتم‌هاست که در سال 2002 توسط Petar Maymounkov و David Mazières طراحی شد. ¹

برخی ویژگی‌های Kademlia که آنرا از دیگر الگوریتم‌ها متمایز کرده اینها هستند:

• استفاده از آدرس هر سیستم (NodeID) هم برای مکانیابی کامپیوترها و هم محتوا
• مرتبه زمانی و فضایی $O(log{n})$؛ یعنی در این الگوریتم فقط با ذخیره 64 رکورد در هر کامپیوتر میتوان 18 اگزا (18 کوینتیلیون) کامپیوتر را در شبکه مدیریت کرد.
• مقاومت ذاتی در برابر حملات DoS؛ شبکه Kademlia قابلیت خود درمانی دارد و حتی در شرایطی که تعداد زیادی از اعضا از دسترس خارج شوند میتواند همچنان فعال بماند.
• نسخه‌هایی از Kademlia وجود دارد که حتی در برابر حملات جعل هویت (Sybil) هم مقاوم هستند.

الگوریتم Kademlia در سیستم‌های توزیع شده مهم و معروفی مثل بیت‌تورنت، اتریوم، I2P، IPFS، و … استفاده میشه و هر کدوم اینها هم تغییراتی در نسخه اصلی ایجاد کردن.

کادملیا چطور کار میکند

خیلی از سیستم‌های DHT ساختارمند برای جاگذاری و مکانیابی گره‌ها و محتواها از یک تابع فاصله (Distance Function) استفاده می‌کنند (مثلا Chord از تابع تفریق معمولی برای محاسبه فاصله استفاده می‌کند). کادملیا از تابع XOR استفاده می‌کند. استفاده از XOR بخاطر چند ویژگی مهم آن است:

• از نظر محاسباتی سبک و سریع است
• فاصله هر node با خودش صفر است
• فاصله A تا B و B تا A برابر می‌شود (اگر در ساختار داده دایره‌ای 10 تایی مجبور باشیم همیشه در یک جهت حرکت کنیم با استفاده از تفریق معمولی برای رسیدن به از نقطه 1 به 2 فاصله می‌شود 1 اما از 1 به 10 با وجودی که کنار هم هستند فاصله می‌شود 9)
• از نابرابری مثلثی پیروی می‌کند (فاصله مستقیم دو گره همیشه کوتاه‌ترین فاصله است)

روش کادملیا برای رسیدن به مقصد نهایی اینطور است که هر سعی می‌کند با طی کردن تعدادی گام که همیشه در بدترین حالت به اندازه لگاریتم حداکثر گره‌های شبکه است به مقصد نزدیک و نزدیکتر شود تا در نهایت آدرس دقیق آنرا به دست آورد.

مثل خیلی از DHT ها کادملیا هم برای ذخیره محتوا id مربوط به node و محتوا را محاسبه می‌کند (هر دو به یک روش) و محتوا در گره‌ای که id اش با id محتوا کمترین فاصله را بر اساس تابع فاصله مورد استفاده (در مورد کادملیا XOR) دارد، ذخیره می‌شود.

پیام‌ها

از آنجایی که کادملیا یک الگوریتم توزیع‌شده است، گره ‌ها باید با استفاده از یکی از روش‌های RPC با یکدیگر صحبت کنن. این روش میتونه هرچیزی باشه. کلا 4 پیام اصلی وجود داره:

• PING: برای بررسی فعال بودن یک گره
• STORE: درخواست ذخیره زوج‌مرتب (کلید، محتوا)
• FIND_NODE: گیرنده این پیام چند گره که از نظر اون نزدیک‌ترین گره‌ها به گره درخواست شده هستند را برمیگردونه
• FIND_VALUE: مشابه STORE عمل می‌کند با این تفاوت که اگر گیرنده کلید درخواست شده را در دیتای ذخیره شده خودش داشته باشه اونو برمی‌گردونه

وقتی پروسیجر STORE فراخوانی می‌شود کادملیا باید مقادیر را در چند گره ذخیره کنه تا اگر یکی از گره‌ها از دسترس خارج شد محتوای آن همچنان در شبکه وجود داشته باشد.

جدول مسیریابی

جدول مسیریابی که کادملیا استفاده می‌کند تا آدرس گره‌ها را به دست آورد یک لیست n تایی است (n برابر اندازه فضای آدرس است، در نسخه استاندارد این عدد 160 بیت است که یعنی 160 رکورد داریم). به هر رکورد این لیست یک k-bucket گفته میشه که عدد k یک عدد انتخابیه که به عنوان تنظیمات گره مشخص میشه (عدد معمول 20 است ¹). نحوه پر کردن جدول مسیریابی کادملیا اینطوریه که اطلاعات گره‌های با فاصله بین $2^i$ تا $2^{i+1}$ در رکورد i-ام ذخیره میشه. مشخصه یک جدول با k-bucket های 20 تایی نمیتونه کل node ها رو ذخیره کنه (و کل نکته DHT هم همینه که آدرس همه رو ذخیره نکنیم)، برای همین انتخاب آدرس‌های ذخیره شده از یک قاعده پیروی میکنه.

قاعده اینطوریه که هر زمان پیامی از یک گره در شبکه دریافت بشه کادملیا سعی میکنه آدرسش رو در جدول مسیریابی‌اش ذخیره کنه. اول فاصله گره حساب میشه تا اندیس مناسب انتخاب بشه ($i=\lfloor log(d) \rfloor$). بعد اگر id در آن k-bucket نباشه و جای خالی هم وجود داشته باشه id به آخر لیست اضافه میشه. اگر از قبل id وجود داشته باشه به آخر لیست منتقل میشه، و اگر k-bucket جای خالی نداشته باشه اولین عضو توسط پیام PING چک میشه، اگر جواب داد همین عنصر به آخر لیست منتقل میشه و گره جدیدی که پیام داده هم نادیده گرفته میشه و اگر جواب نداد اولین عنصر حذف میشه و id جدید به آخر لیست اضافه میشه.

این قاعده باعث می‌شود گره‌هایی که اخیرا دیده کمتر دیده شده اند و در دسترس نیستند از لیست حذف شوند اما گره‌هایی که قدیمی‌تر هستند به گره‌های جدیدتر ترجیح داده شوند. این قاعده دو دلیل دارد. اول اینکه گره‌های قدیمی‌تر قابل اعتمادتر هم هستند و ثبات بیشتری دارند در نتیجه ترجیح آنها باعث ثبات بیشتر شبکه خواهد شد. دوم اینکه چنین قاعده‌ای شبکه کادملیا رو نسبت به حملات DoS مقاوم میکنه، چون نمیشه با ارسال پیام‌های جعلی باعث اخراج گره‌های معتبر از جدول مسیریابی شد.

عملیات جستجو

عملیات جستجو هم بسیار ساده است. کادملیا به صورت Iterative سعی می‌‌کند اطلاعات گره‌ای که نمیشناسد را از نزدیکترین گره موجود در شبکه به آن بپرسد. نکته اینه که کادملیا این کار را به صورت Iterative انجام میده (یعنی همان گره اول تمام سوالات تا آخر رو میپرسه و متکی به بقیه گره‌ها نمیمونه تا اونا گره مقصد رو پیدا کنن، اینطوری بهینه سازی سرعت در کادملیا خیلی راحتتر انجام میشه و شرایطی که بدون پیشرفت صرفا منتظر جواب بقیه باشه پیش نمیاد).

برای اینکار کادملیا اول $\alpha$ گره از k-bucket مربوط به گره مقصد را انتخاب میکنه (عدد $\alpha$ یک عدد انتخابی و قابل تنظیم در نرم‌افزاره؛ عدد 3 یک عدد معمول است ¹). اگر k-bucket مربوطه $\alpha$ تا عضو نداشته باشه به اندازه $\alpha$ از نزدیکترین رکوردهای دیگه برمی‌داریم.

بعد یک درخواست RPC از نوع FIND_NODE به گره‌های انتخاب شده ارسال میشه و اونا موضف اند k گره نزدیک خود که در k-bucket اش به گره مقصد مورد نظر دارن را به عنوان جواب برگردونن. این جواب ها در یک لیست که به ترتیب فاصله گره‌های جواب تا گره مقصد مرتب میشه ذخیره میشن.

حالا اگر توی آخرین جواب گره جدیدی به لیست اضافه شده باشه درخواست FIND_NODE به $\alpha$ گره‌ای از بین لیست k تایی که قبلا دیده شدن ولی درخواستی بهشون ارسال نشده ارسال می‌کنه. وگرنه اینکارو برای همه گره‌هایی از بین کل k گره انجام میده که درخواستی بهشون ارسال نشده.

وقتی به همه گره‌ها درخواست ارسال شد و جوابشون دریافت شد چرخه متوقف میشه.

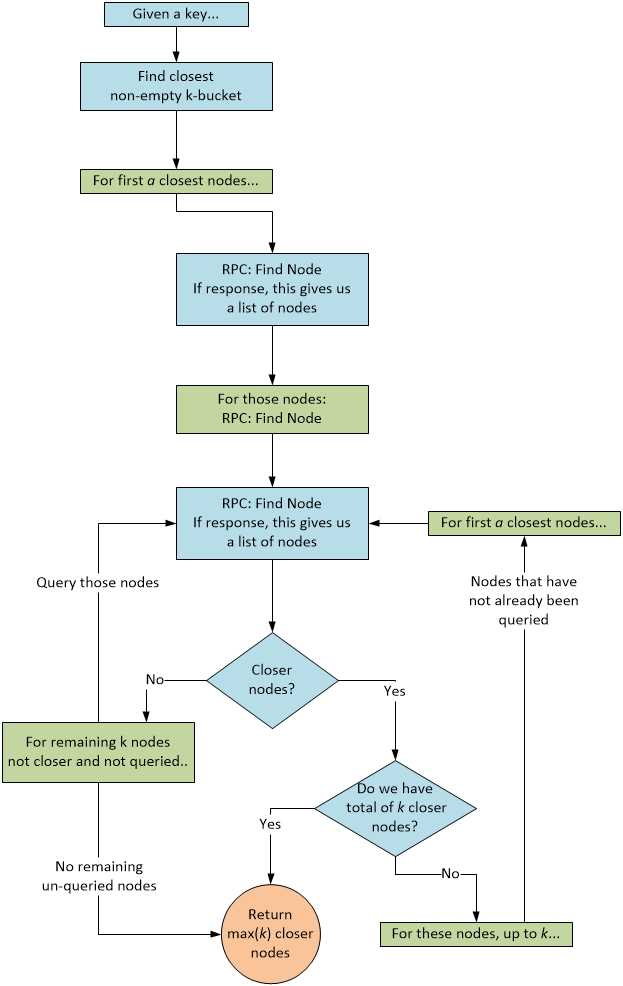الگوریتم جستجوی گره در کادملیا

راه‌اندازی اولیه (Bootstraping)

یکی از مسايل پیوستن به شبکه‌ای که با DHT کار میکنه پیدا کردن نقطه ورود است. همونطور که از ساختار جدول مسیریابی هم مشخصه شبکه بین گره‌هایی ساخته میشه که همدیگه رو میشناسن، در واقع اگر میشه چندین شبکه کادملیا داشت که چون از نظر گراف به هم متصل نیستن (هیچ گره ای ادرسی از گره دیگه ای در شبکه دوم در جدول مسیریابی‌اش نداره) در واقع چند شبکه جدا به حساب میان (و طبیعتا میتونن در هر لحظه به هم متصل بشن).

اگر در یک شبکه خصوصی بخواهیم Gateway رو پیدا کنیم مشکل خاصی پیش نمیاد و احتمالا از طریق یک روش جانبی آدرس رو با هم به اشتراک میذاریم اما اگر بخواهیم به یک شبکه عمومی شناخته شده مثل تورنت یا I2P متصل بشیم شبکه باید روشی برای پیدا کردن گیتوی هم ارائه کند، مثلا در تورنت آدرس‌های ثابتی وجود داره که کلاینت‌ها با اتصال به اونا نقطه ورود پیشنهادی رو دریافت میکنن (روی این آدرس‌ها نرم افزار خاصی برای این کار سرویس میده):

• router.bittorrent.com:6881
• router.utorrent.com:6881 (uTorrent)
• dht.transmissionbt.com:6881 (Transmission)
• router.bitcomet.com:6881 (BitComet)
• dht.aelitis.com:6881 (Vuze)

برای ورود به شبکه‌های DHT در حال حاضر حتما باید گره‌ای که قبلا در شبکه هست رو به عنوان نقطه ورود (Bootstrap Node) بشناسیم، یعنی آدرسش رو داشته باشیم. طبیعتا اگر بدون دونستن آدرس گره دیگه‌ای در یک شبکه یک سیستم DHT ران کنیم مثل اینه که یک شبکه جدید ساختیم و دیگران باید بهش متصل بشن.

پس دو حالت پیش میاد یا بدون بوت‌استرپ شبکه را اجرا میکنیم و یک شبکه جدید تشکیل میدیم، یا یکی را در شبکه دیگه‌ای که فعال است رو میشناسیم و به اون برای ورود درخواست میدیم.

فرایند بوت‌استرپ به این شکل است که گره ورودی (Gateway) را در k-bucket مناسب‌اش وارد میکنیم. بعد یک جستجو برای خودمون (Self Node Lookup)، طبیعتا تنها کسی که میشناسیم گیتوی است و در نتیجه این جستجو از طریق اون نزدیک‌ترین گره‌ها به خودمون رو پیدا خواهیم کرد (نود‌های بین خودمون و گیتوی). در نهایت یک جستجوی in-range برای همه k-bucket های بعد از کوچکترین رکورد غیر خالی اجرا میکنیم (یعنی یک ادرس رندم که فقط در محدوده اون k-bucket باشه رو جستجو میکنیم).

این فرایند علاوه بر پر کردن جدول مسیریابی خود گره جدید او را به بقیه گره‌ها هم معرفی می‌کند تا در صورت لزوم در جدول آنها هم قرار بگیرد.

ذخیره و بازیابی اطلاعات

سیستم کادملیا یک Hash Table است، در نتیجه هر داده‌ای برای ذخیره یا بازیابی یک کلید لازم داره و ما زوج مرتب‌های $<key, value>$ را ذخیره میکنیم. در کادملیا کلید گره‌ها و مقادیر با یک روش ساخته می‌شوند و مشابه هم هستند. برای هر پروسیجر درخواست ذخیره‌سازی و یا بازیابی اطلاعات یک پروسیجر جستجو (Node Lookup) برای کلیدش اجرا می‌شود.

برای ذخیره زوج مرتب‌ها بعد از پروسیجر FIND_NODE یک پروسیجر STORE روی همه جواب‌های آن اجرا می‌شود. این پروسیجر در واقع به آن گره‌ها دستور ذخیره مقدار مورد نظر ما را می‌دهد. در سیستم کادملیا سه نوع ذخیره‌سازی وجود دارد:

• Original Publisher Store: دیتای تولید شده توسط خود گره که هر 24 ساعت مجددا در شبکه توزیع می‌شود
• Re-Publisher Store: دیتای توزیع شده توسط دیگران که هر یک ساعت مجدد توزیع می‌شود
• Cahce Store: دیتای کش شده در فرایند جستجوی دیتا که در نزدیک ترین گره ذخیره میشود، میتواند تاریخ انقضا داشته باشد و هیچ وقت توزیع نمی‌شود

برای بازیابی مقدار یک کلید از DHT هم پروسیجر جستجو اجرا می‌شود با این تفاوت که بجای پروسیجر اصلی جستجو (FIND_NODE) ، پروسیجر FIND_VALUE اجرا می‌شود. تنها تفاوت این پروسیجر با پروسیجر FIND_NODE آن است که گره دریافت کننده اگر مقدار مورد نظر که کلیدش ارسال شده را داشته باشد مقدار را برمی‌گرداند، وگرنه مثل FIND_NODE عمل کرده و k گره نزدیک به کلید جستجو شده که می‌شناسد را برمی‌گرداند. بعد از پیدا کردن دیتا گره جستجو کننده مقدار را در نزدیکترین گره‌ای که برای پیدا کردن مقدار به آن درخواست داده و موفق نشده ذخیره می‌کند و به این ترتیب سرعت درخواست‌های بعدی بالا رفته و مقادیر به گره‌های اصلی که باید در آن ذخیره می‌شدند و احتمالا در زمان ذخیره سازی در دسترس نبودند نزدیک می‌شوند.

عملیات نگهداری شبکه

• محتوای تولید شده توسط خود گره هر 24 ساعت مجددا در شبکه توزیع می‌شود
• محتوای توزیع شده توسط دیگران هر یک ساعت مجددا توزیع می‌شود
• طول عمر هر دیتای توزیع شده توسط دیگران با تعداد گره‌ها بین گره فعلی و نزدیکترین گره به محتوا رابطه معکوس دارد و باید هر بار که گره جدیدی به شبکه اضافه می‌شود مجدد حساب شود
• هر زمان گره جدیدی به k-bucket اضافه می‌شود، اگر به محتوای ذخیره شده‌ای نزدیکتر از دیگران بود باید محتوای مربوطه روی آن بازنشر شود
• اگر یک k-bucket برای یک ساعت هیچ جستجویی نداشت باید رفرش شود. به این شکل که یک جستجوی غیر واقعی روی آن اجرا شود

ادامه دارد …

منابع

• A Brief Overview of Kademlia, and its use in various decentralized platforms
• Distributed Hash Tables with Kademlia
• TinyTorrent: Implementing a Kademlia Based DHT for File Sharing

1. Kademlia: A Peer-to-peer information system based on the XOR Metric- The Kademlia Protocol Succinctly ↩ ↩² ↩³